1 HW 7-1
1.1 估算行星质量
将行星 和恒星 视为双星系统,两者距离为 ,对于近似圆周运动,视向速度为三角函数,满足:
双星的角速度容易根据万有引力 向心力算出为:
于是结合上述两式,消去其中的 可得到:
得到
1.2 势散射
见朗道力学
前情提要

(a)

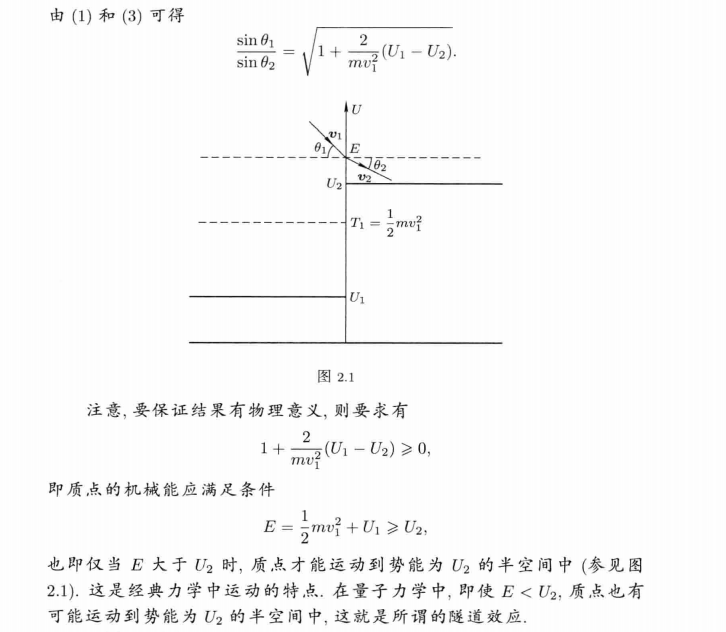
(b)
朗道书中, 是散射角。
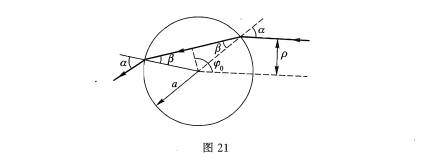




ps:上面的从(7)式往后的繁琐积分是没必要的,因为 ,确定 最大可取为 后,其积分显然为 。
1.3 有心力场
改作业时发现很多同学竟然不会用 判断轨道是否有界,这是力学的内容。已知
所以
- 假设 ,所以朝着物体移动的方向: 增大的方向,若 也即 增加就意味着 ,即速度减小,粒子被束缚。
- 假设 ,所以朝着物体移动的方向: 减小的方向,若 也即 增加就意味着 ,即速度减小,粒子被束缚。
上述的情形对应如下图片当中 的片段:
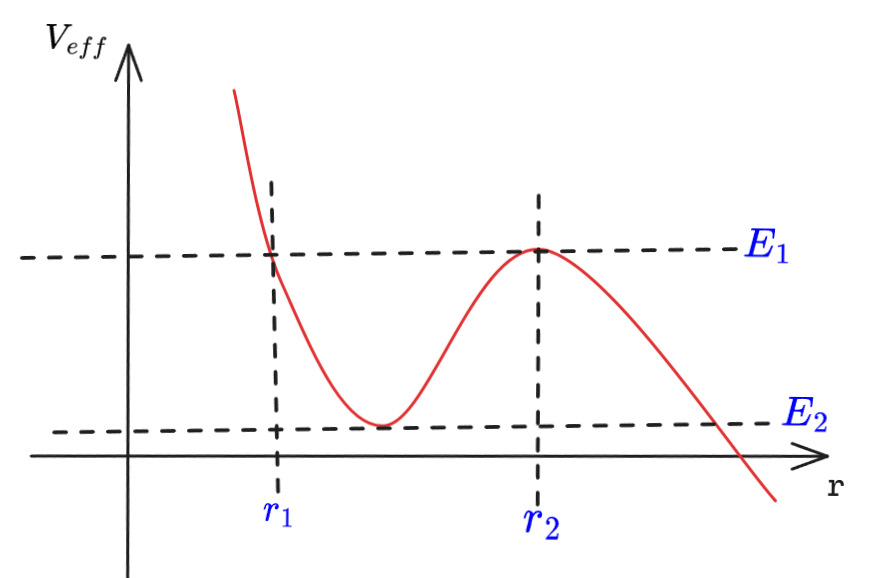
画一条水平线,它的纵坐标为 ,因为 ,所以若此时 曲线在该水平线下侧,那么水平线与 曲线的差距就是径向动能 ,所以若初始时轨道在 的片段,那么运动就无法跨过区间两侧的势垒,否则 ,物体被束缚。
若刚好 ,那么物体就只能待在极小值点,也就是做圆轨道运动。若 并且从 开始运动,那么就可以轻而易举地跨越势垒,导致运动无界。若 ,但物体没有运动到被束缚的区间 ,而是运动在 ,那么朝着 增大的方向,径向动能 越大,轨道也是无界的。开普勒运动中,就是这样来区分三种轨道的。
因为切换大小写过于麻烦,所以以下讨论用 代替 ,约化质量 代替 .
我们使用 binet 微商方程,做如下换元:
那么
同时能量守恒给出:
整理第二个等号得到:
改写为:
该方程可分离变量求解,得到:
做换元 并取 可发现上式为圆锥曲线方程,其离心率满足:
离心率 ,或者说 的正负(排斥或吸引势),将确定轨道的形状。注意 不但大于 ,还要小于 (因为上式为平方根,要大于 0)。
此外,本题选用拉格朗日方程的方法可更快得到结果。(采用直角坐标,发现拉格朗日方程就是简谐振动方程)
假设 。如果物体的瞄准距离 大于 , 显然只会(1)在球外做直线运动,反之,轨道(2)在球内发生折射或者(3)被束缚在球内。
一般来说,可以分三种情形绘制如下 ,以此确定轨道的有界还是无界,注意对于球外的物体,穿过球体的条件 等价于 (对应于下图紫色区域,即 )
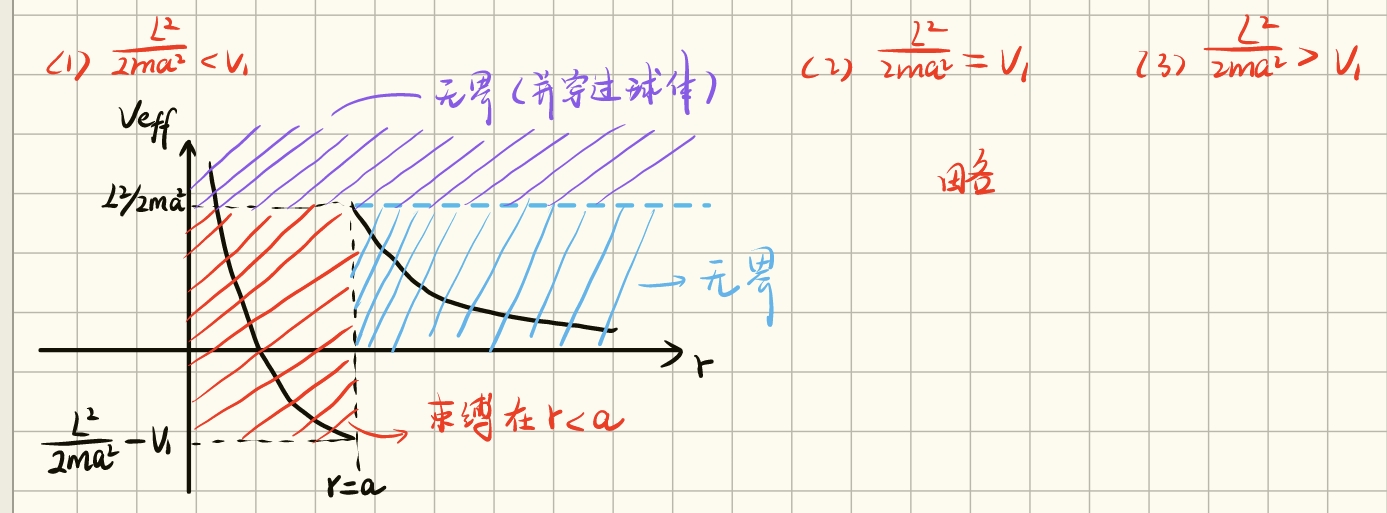
(c) 反比力
见 HW6的T2,根据 和 的正负可确定轨道形状。通过 作图可以进一步确认轨道是否有界。
对于 ,有
令 , 可以得到对应圆轨道的半径,在常见情形下(),该方程有 0~2 个根(对应 有 0~2 个极值点)。据此可以画出 的图像,根据直线 在途中的位置,可以将轨道分为几种类型:
- 无界(类似抛物线/双曲线但与之偏离。或者从无穷远入射,环绕几圈后再返回无穷远);
- 进动(类椭圆轨道的进动);
- 圆(特殊情形,但处于势能极大时容易不稳定)。
所以根据 根的个数得到如下图:
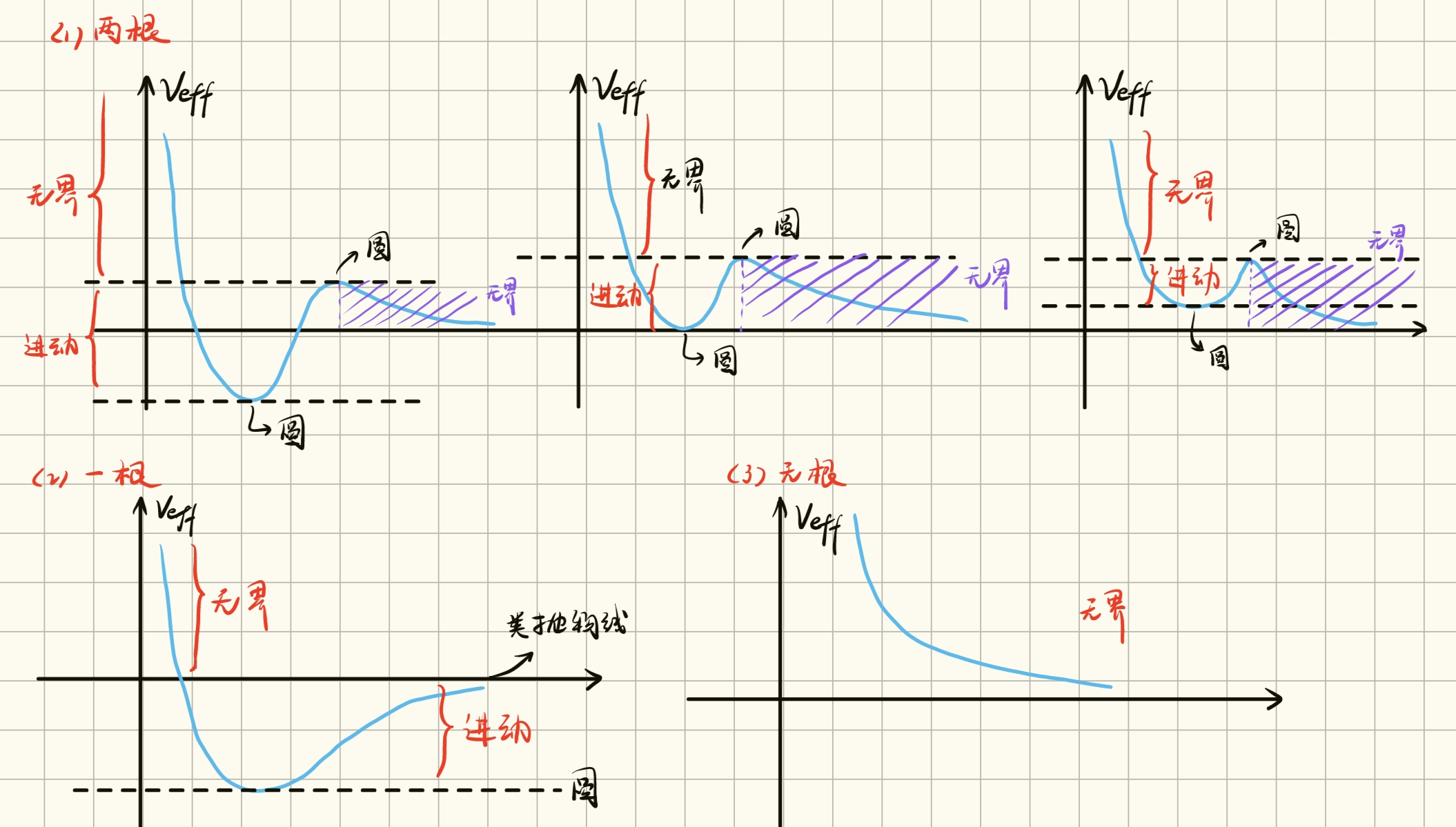
对于最常见的第一种情形, 在 区间上被 的两个极值点 分割,符号变化为 , 的极大值点由 得到, 为 ,由上述几个曲线可知,要使得轨道有界,必须存在 或者说存在 成立,那么必须有
于是得到
若上式不成立,则轨道无界。反之,三种情况都有可能。
2 HW 7-2
2.1 三维各向同性谐振子
(a)
将 替换为 , 替换为约化质量 ,可得到与 HW7-1第三题(a) 一致的结果。题目要求用积分求解,助教在这里偷个懒,就不细算了。
(b)
取 ,以及:
代入 得到:
或者,
这保证了轨道是椭圆(),联立后两式可得:
(c)
面积速度是
而熟知的椭圆面积是
于是得到
而对于求解 ,根据 有:
看了一眼题目给的结果,选择做换元 得到
因为分母当中 ,所以只有唯一解:
2.2 势散射
(a)
与 HW7-1第2题(a) 同理,不赘述。
(b) (c)
题目中的碰撞参数 是瞄准距离,此题与 HW7-1第2题(b) 相同,两者的结果分别是 HW7-1第2题(b) 的(5)式和(6)式。
2.3 (a)
此题对应于 HW6第二题的第一种情形,对当时给出的结果做一下字母替换,得到同样适用于本题的结论:
(b) (c)
见朗道力学: